(x y)^2-4xy formula 231330-(x+y)^2-4xy formula

Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorShare with your friendsAnswer (1 of 2) For the homogeneous equation (x^2 2y^2)dx (4xy y^2)dy =0 take y = xV(x) so dy = Vdx xdV The equation becomes (1 6V^2 V^3)dx x(4V V^2)dV =0 Separating (3V^2 12V)dV/3(v^3 6V^2 1) = dx/x or (1/3)d(V^3 6V^2 1) = dx/x Integrating ln(V^3 6V^2

A Opq Is Formed By The Pair Of Straight Lines X 2 4xy Y 2 0 And The Line Pq The Equation Of Pq Is X Y 2 0 Sarthaks Econnect Largest Online Education Community

(x+y)^2-4xy formula

(x+y)^2-4xy formula-The differential equation (2xy y^2 y) dx (3x^2 4xy 3x) = 0 is Exact and NonHomogeneous Exact and Homogeneous NonExact and Homogeneous NonExact and NonHomogeneous Solve x dy y dx = 2xy^2 dx x^3 = cy O x^3 y =c O x^3 = cy^2 O x^3 y^2 =c 21A an equilateral triangle B a right angled triangle C an isosceles triangle D None of these Answer A Solution Acute angle between the lines x^24xyy^2=0 is tan^2 (2sqrt (41))// (11)=tan^ (1)sqrt (3)=tan^ (1)pi//3 Angle bisectors of x^24xyy^2=0 are given by (x^2y^2)/ (11)= (xy)/ (2) x^2y^2=0rArr x=y As xy=0

Solved A Simplify I 8x 3y 2 4xy Ii 25x 4y 3 5x 2 Y 7 B I 1 Answer Transtutors

Canonical form of a double hyperboloidNote We don't even have to consider the formula (xy)^2 = (xy)^24xy as in other problems and then find (xy) for solving the values of x and y because from (*) we have already concluded that one of x or y is ZERO and so if we take y= 0 and put it in (2),we get (it orally even) that x=3The joint (combined) equation of the lines OA and OB is x 2 4xy y 2 = 0 and the equation of the line AB is 2x 3y 1 = 0 ∴ points A and B satisfy the equations 2x 3y 1 = 0 and x 2 4xy y 2 = 0 simultaneously We eliminate x from the above equations, ie, put x = `(1

Description for Correct answer \( \Large cos^{2} \theta =\frac{(xy)^{2}}{4xy} \) max value of \( \Large cos^{2} \theta =1 \) \( \Large \Rightarrow 1=\frac{(xy)^{2Here $M= x^24xy2y^2 $ & $ N= y^24xy2x^2 $ $\dfrac {\partial M}{\partial y}=04x4y$ $\dfrac {\partial N}{\partial x}=04y4x$ Here, $\dfrac {\partial M}{\partial Use the quadratic formula to solve the equation for (a) x in terms of y and (b) y in terms of x Homework Equations 4x^2 4xy 1 y^2 = 0 The Attempt at a Solution I am not really sure where to start at all If I could just figure out the values for a, b, and c of the quadratic formula then the rest would be simple (for me)

  Your differential equation is of the form M (x,y) dx N (x,y) dy = 0 with dN/dx = dM/dy (those being partial derivatives) The last equation is a necessary and sufficient condition for a solution of the form f (x,y) = 0 In your case df/dx (partial) = x^2 4xy 2y^2 andX 2 y 2 = (x – y) 2 2xy Algebraic identities The algebraic equations which are valid for all values of variables in them are called algebraic identities Factorise (x y)^24xy9z^2 (4 • (x 2)) 3 2 y 2 Step 2 Equation at the end of step 2 2 2 x 2 3 2 y 2 Step 3 Trying to factor as a Difference of Squares 31 Factoring 4x 29y 2 Favorite Answer x^2xy y^2 this equation can't be factor because there is no two numbers whose product and sum is one RealArsenalFan Lv 4 1 decade ago You

3 5 Points Consider The Differential Equation Itprospt

Show That The Lines X 2 4xy Y 2 0 And X Y 10 Contain The Sides Of An Equilatera Youtube

Please be sure to answer the questionProvide details and share your research!Combine 2xy and 4xy to get 2xy x^ {2}\left (2y\right)xy^ {2}=0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtractionTranscribed image text Find the general solution in powers of x of the differential equation (x^2 1)y" 4xy' 2y = 0 Assume the form y(x) = Sigma^infinity _n = 0 c_nx^n Then y'(x) = Sigma^infinity _n = 1 c_nx^n1 y"(x) = Sigma^infinity _n = 2 c_nx^n2 x^2y"(x) = Sigma^infinity _n = 2 c_nx^n y"(x) = Sigma^infinity _n = 0 c_nx^n 4xy'(x) = Sigma^infinity _n = 1 c_nx^n 2y(x) =

Answered Solve The Exact Differential Equation Bartleby

Example 11 Find Particular Solution Dy Dx 4xy2 Examples

Write the equation x 2 4xy y 2 3 = 0;Answer by AnlytcPhil (1761) ( Show Source ) You can put this solution on YOUR website! Pair of Linear Equations in Two Variables (xy)2 = (xy)2 4xy how ?

Factoring Two Variable Quadratics Rearranging Video Khan Academy

3 5 Points Consider The Differential Equation Itprospt

Other calculators Graph of implicit function;(one minus x)y two strokes of the second (2nd) order minus 4xy stroke first (1st) order plus 5y stroke first (1st) order equally co sinus of e of x Similar expressions y'cosx2ycosx=2sinxSolve the following system of equations 3x 4xy 2y = 2 3x 2y = 10 Solve the second equation for either of the unknowns I'll pick x 3x 2y = 10 add 2y to both sides 3x = 10 2y Divide both sides by 3 x = (10 2y)/3 factor out 2 x = 2 (5 y

Selina Chapter 4 Expansions Including Substitution Icse Solutions Class 9 Maths

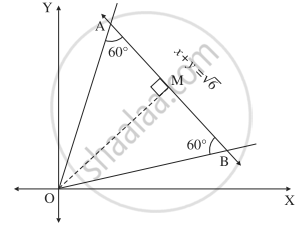
Show That The Lines X2 4xy Y2 0 And The Line X Y 6 Form An Equilateral Triangle Find Its Area And Perimeter Mathematics And Statistics Shaalaa Com

 y = arctan(x)/(1x^2)^2 C/(1x^2)^2 We have (1x^2)y'4xy=(1x^2)^2 A We can rearrange A as follows (1x^2)y'4xy = 1/(1x^2)^2 dy/dx (4x)/(1x^2)y = 1/(1x^2)^3 B We can use an integrating factor when we have a First Order Linear nonhomogeneous Ordinary Differential Equation of the form;Can you see the Eiffel Tower from London? If 2x – y = , then the triangles is 6 If sinθ−cosθ s i n θ − c o s θ = 1 2 1 2 then value of sinθcosθ s i n θ c o s θ is 7 If sinθ cosθ = 1, then the sinθ cosθ is equal to 8 The angle of elevation of the top of a tower from two horizontal points (in opposite sides) at distances of x meter and x 12 meter from the

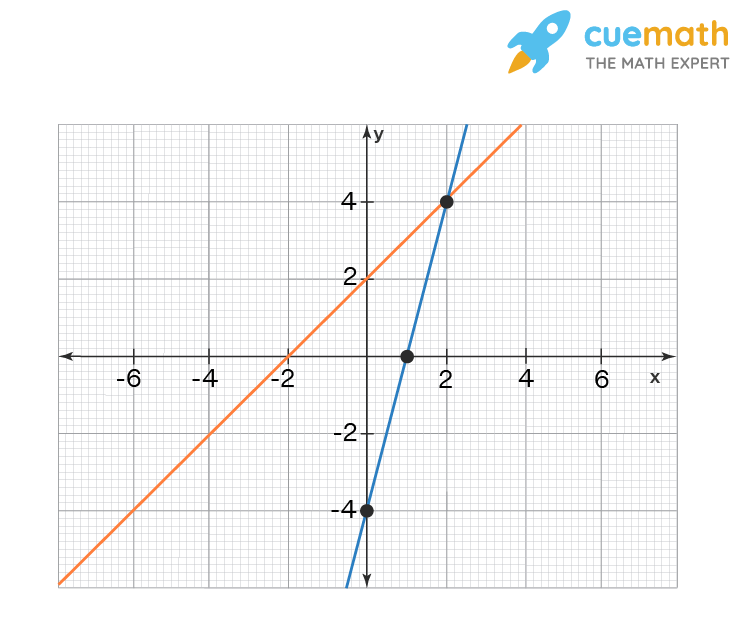
Draw The Graphs Of The Pair Of Linear Equations X Y 2 0 And 4x Y 4 0 Calculate The Area Of The Triangle Formed By The Lines So Drawn And The X Axis

Solved No For The Equation 4x Y Xy 1 X Y 0 We Look Chegg Com

 Thanks for contributing an answer to Mathematics Stack Exchange! Please see below The equation given here x^24xy4y^25sqrt51=0 is of the form Ax^2BxyCy^2DxEyF=0 What a rotation does is it changes x & yaxes to x' & y'axes, as shown below, In such a case, the relation between coordinate (x,y) and new coordinates (x',y') is given by x=x'costhetay'sintheta and y=x'sinthetay'costheta and reverse isSolution for x^24xy3y^2= equation Simplifying x 2 4xy 3y 2 = 0 Reorder the terms 4xy x 2 3y 2 = 0 Solving 4xy x 2 3y 2 = 0 Solving for variable 'x' Factor a trinomial (x y)(x 3y) = 0 Subproblem 1 Set the factor '(x y)' equal to zero and attempt to solve Simplifying x y = 0 Solving x y = 0 Move all terms containing x to the left, all other terms to the right

Complete The Proof Drag And Drop The Expression To Correctly Complete The Proof Of The Polynomial Brainly Com

1

 M = x 2 4xy 2y 2, N = y 2 4xy 2x 2 dM/dy = 4x 4y dN/dx = 4y 4x Therefore, dM/dy = dN/dx So, the given differential equation is exact On integrating M wrt x, treating y as a constant, On integrating N wrt y, treating x as a constant, (omitting 2xy 2 2x 2 y which already occur in ∫M dx) Therefore, the solution ofAnswer (1 of 4) y' = x 4xy Here are two basic methods to solve first order differential equations I'd choose separation of variables to solve this one more quickly 1 linear first order DE y' 4xy = x, \rho(x) = exp(\int 4x dx) = e^{2x^2} 2 separation of variables DE \frac{dy}{dx} =Surface defined by equation;

The Line X 2 4xy Y 2 0 And X Y 4 Are The Sides Of An Equilateral Triangles Whose Area Is Equal To A 3 1 2 Then A Is Equal To Sarthaks Econnect Largest Online Education Community

If A Represents The Area Of The Ellipse 3x 2 4xy 3y 2 1 Then The Value Of 3 5 Pia Is

Bx" yp = Use reduction of order to find the general solution in this form (your answer will involve A, B, and x) y (2) =Related Links sec h (πi) cosec h (π / 2)i = sec 2 (tan1 2) cosec 2 (cot1 3) = Select the right option in the following Set A has m elements and set B has n elements If the total number of subsets of A is 112 more than the total number of subsets of B, then the value of m×n isIf the equation 2x^2 4xy 7y^212x2yt=0 where "t' is a parameter has exactly one real solution of the form (x,y)Then the sum of (xy) =?

X2 Y2 2 4xy Find Dy Dx Mathematics Topperlearning Com 6729

Solved Lot F X Y Xy 2 4xy 2x Y Find The Equation Chegg Com

Example 1 Determine the critical points and locate any relative minima, maxima and saddle points of function f defined by f(x , y) = 2x 2 2xy 2y 2 6x Solution to Example 1 Find the first partial derivatives f x and f y f x (x,y) = 4x 2y 6 f y (x,y) = 2x 4y The critical points satisfy the equations f x (x,y) = 0 and f y (x,y) = 0 simultaneously HenceSolve the equation Solution This is a Bernoulli equation with the parameter Therefore, we make the substitution The derivative is given by Multiply both sides of the original equation by and divide by Notice that in dividing by we have lost the solution Rewriting the last equation in terms of we get This differential equation is linear, soSolution(By Examveda Team) $$\eqalign{ & {\cos ^2}\theta = \frac{{{{\left( {x y} \right)}^2}}}{{4xy}} \cr & {\text{Max value of }}{\cos ^2}\theta = 1 \cr

Sec 28 4xy X Y 2 Is True If Any Only If Sarthaks Econnect Largest Online Education Community

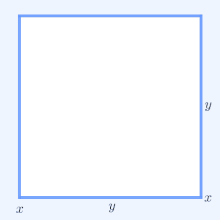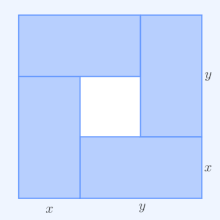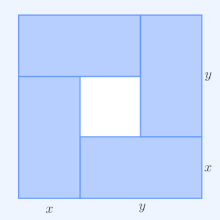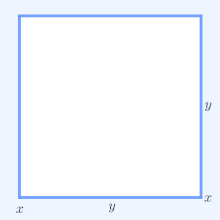
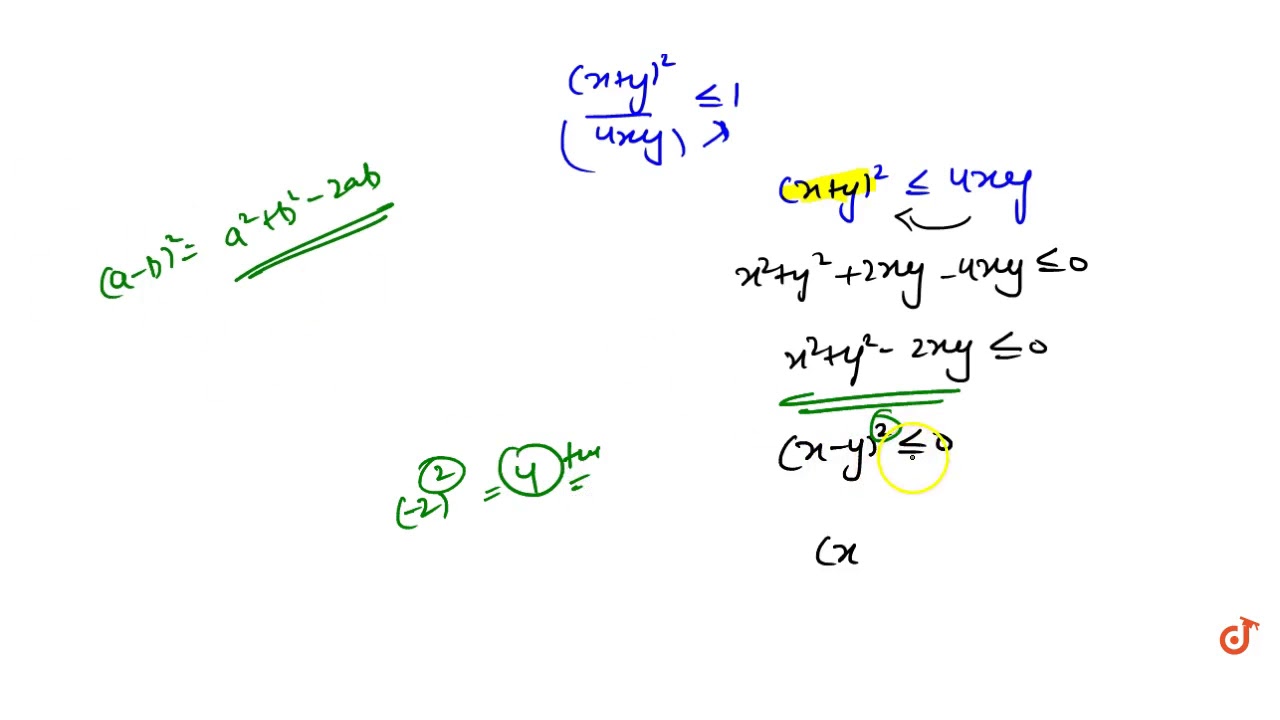
Inequality Of Arithmetic And Geometric Means Wikipedia

Thanks for contributing an answer to Mathematics Stack Exchange! First we have to solve the homogeneous equation (31) x 2 y" − 4xy' 6y = 0 This is an EulerCauchy equation, so we look for solutions of the form y = x mThe characteristic equation for m is∴ x 2 4xy y 2 = 0 is the joint equation of the two lines through the origin each making an angle of 60° with x y = 10 ∴ x 2 4xy y 2 = 0 and x y = 10 form a triangle OAB which is equilateral

Mathematics X42 Draw The Graphs Of The Pair Of Linear Equations X Y 2 0 Andcalculate The Area Of The Triangle Formed By The Lines So Drawn And The X Axis 4x Y 4 0 Ncertexemplari Snapsolve

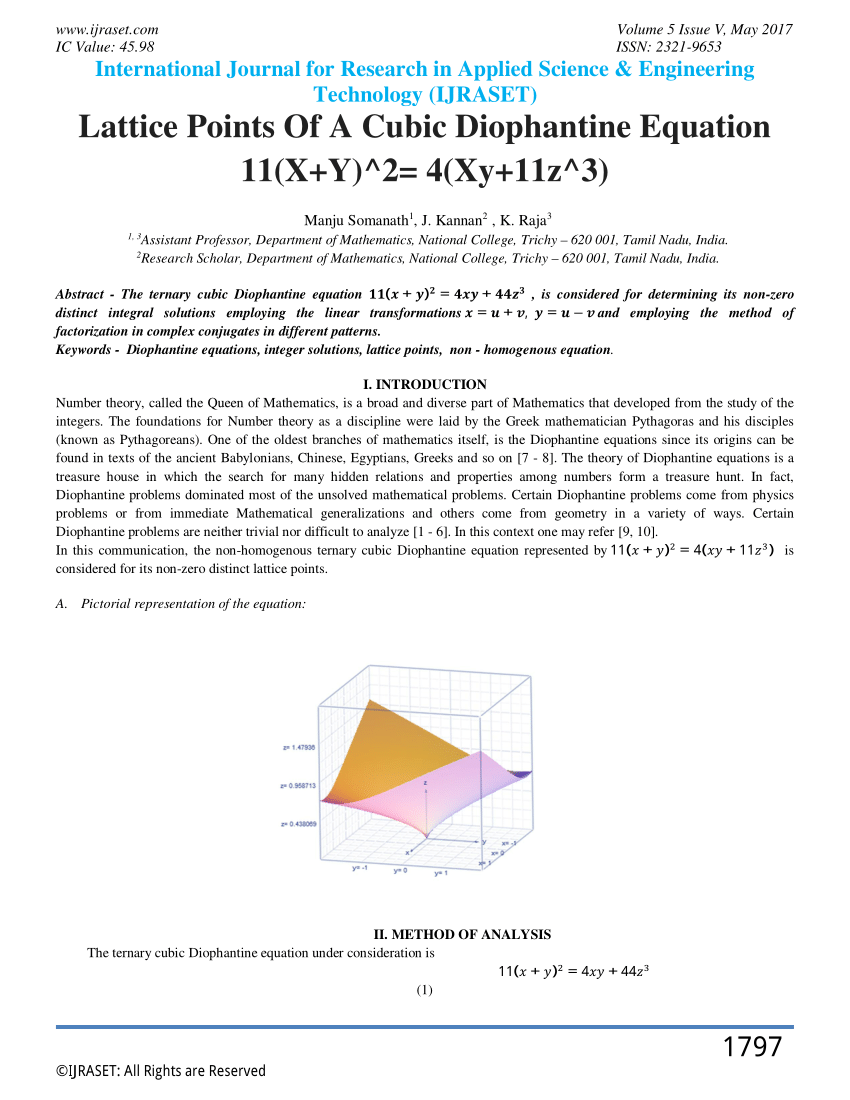
Pdf Lattice Points Of A Cubic Diophantine Equation 11 X Y 2 4 Xy 11z 3

 Find an answer to your question factorise X^2 4xy 4y^2 9z^2 AnshuSingh AnshuSingh 1 week ago Mathematics High School answered Factorise X^2 4xy 4y^2 9z^2 1 See answer AdvertisementX24xy4y2 Final result (x 2y)2 Step by step solution Step 1 Equation at the end of step 1 ( (x2) 4xy) 22y2 Step 2 Trying to factor a multi variable polynomial 21 Proof that x^24xyy^2=1 has infinitely many integer solutions Proof that x2 4xyy2 = 1 has infinitely many integer solutions https//mathstackexchangecomY'4xy^2=x Derivatives First Derivative Specify MethodNew Chain Rule Product Rule Quotient Rule Sum/Diff Rule Second Derivative Third Derivative Higher Order Derivatives Derivative at a point Partial Derivative Implicit Derivative Second Implicit Derivative Derivative using Definition Derivative Applications Tangent Normal Curved Line Slope

Symbolic Math How To Solve Exact Differential Equations In Matlab Stack Overflow

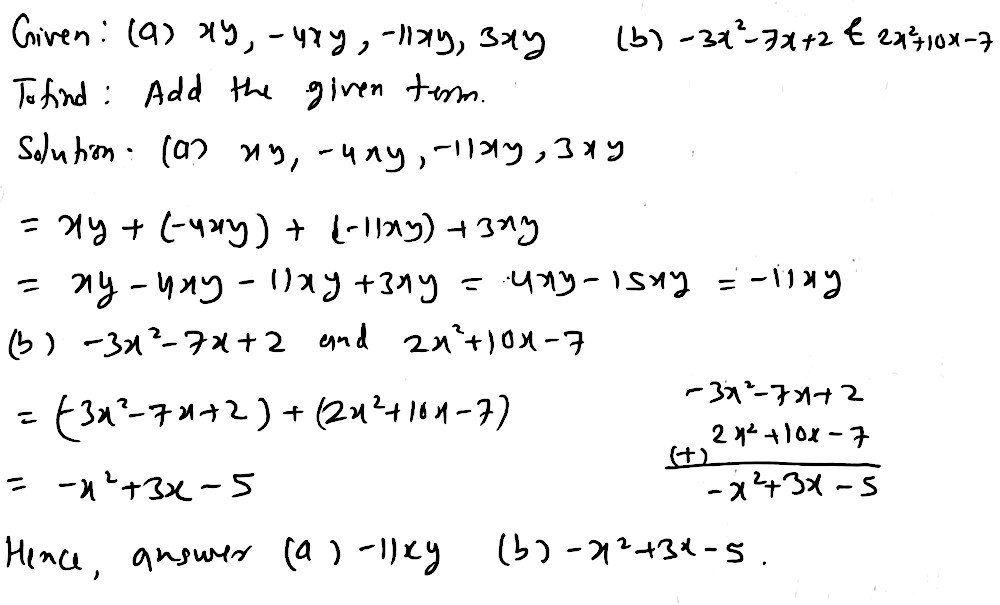
Add The Following A Xy 4xy 11xy 3xy B 3x 2 7x 2 And 2x 2 10x 7 Snapsolve

Please be sure to answer the questionProvide details and share your research!Examine the function f (x,y) = y2 4xy 3x2 x3 for extreme values written 10 months ago by teamques10 ♣ 16k modified 3 months ago by binitamayekar ♣ 25k engineering mathematics ADD COMMENT EDIT 1 Answer Find dy/dx by implicit differentiation x2 − 4xy y2 = 4 x24xyy2=4 Maybe you like Identify the surface whose equation is given?

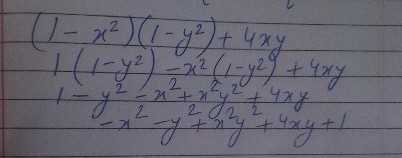
Factorise 1 X 2 1 Y 2 4xy Scholr

X 1 2 3 And Y 1 2 3 Then The Value Of X 2 4xy Y 2 X Y Mathematics

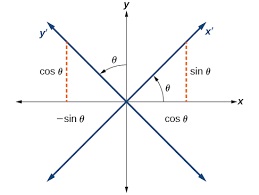
Simplifying X 2 4xy y 2 = 0 Solving X 2 4xy y 2 = 0 Solving for variable 'X' Move all terms containing X to the left, all other terms to the right Add '4xy' to each side of the equationThe equation x y = 4 and x^2 4xy y^2 = 0 represent the sides of Question The equation x−y=4 and x 24xyy 2=0 represent the sides of A an equilateral triangle B a right angled triangle C an isosceles triangle D none of these Medium Solution Verified by Toppr Correct option is A an equilateral triangle Given sides x 24xyy 2=0⇒y 24xyx 2=0θ = 45° in terms of a rotated x′y′system using θ, the angle of rotation Write the equation involving x′ and y′ in standard form

Solved Find The Arc Length Of The 24xy Y 4 48 From Y 2 To Y 4 Course Hero

Answered Consider The Following 2x2 4xy 2y Bartleby

 (xy)^2 (xy)^2=4xy identity is the equation?Hello student, Pl Book a Trial With Our ExpertsClick here👆to get an answer to your question ️ The equation x^2 4xy 4y^2 3x 6y 4 = 0 represents a Solve Study Textbooks Guides Join / Login Question The equation x 2 4 x y 4 y 2 The equation λ x 2 4 x y y 2

Calc3 1001 By James Bardo Issuu

Answered 1 Consider The Following Quadratic Bartleby

Popular Problems Calculus Find dy/dx x^24xyy^2=13 x2 4xy y2 = 13 x 2 4 x y y 2 = 13 Differentiate both sides of the equation d dx (x2 4xy y2) = d dx (13) d d x ( x 2 4 x y y 2) = d d x ( 13) Differentiate the left side of the equation Tap for more steps DifferentiateBut avoid Asking for help, clarification, or responding to other answersExplanation Step 1 1 of 5 (a) We can detect the linear dependency of the functions by graphing them \\\\ all on the coordinate axes, and see if they are multiple of each other or not \\\\ Below are the graphs of both the functions y 1 = x 3 \\\\ {\color {#c} y_1=x^3}\quad y 1 = x 3

For Questions 61 I Got A But For Question 62 I Don T Know How To Simplify Any Further Than 6x 2 9xy 3y 2 2y X 3 I Tried Using The Qudratic Formula For The Top And Got X 0 5y

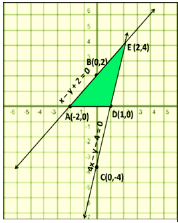
Draw The Graphs Of The Pair Of Linear Equations X Y 2 0 And 4x Y 4 0 Calculate The Area Of The Triangle Formed By The Lines So Drawn And The X Axis Snapsolve

Given yı (2) = x² satisfies the corresponding homogeneous equation of = z'y" – 4xy' by = 6x – 12, x > 0 Then the general solution to the nonhomogeneous equation can be written in the form y (x) = Ax?Write logically 2 See answers Advertisement Brainly User Hello user Expanding the LHS we get (xy)^2 (xy)^2 x^2y^2 2xy x^2y^2 2xy 4xy =RHS Hence proved Advertisement harendrachoubay , verified Stepbystep explanation We have, Verify, LHS Using algebraic identity, and = 4xyBut avoid Asking for help, clarification, or responding to other answers

If Cosec 2 Theta 4xy X Y 2 Then Find The Relation Between X And Y Mathematics Topperlearning Com R0vcgjee

Solved A Simplify I 8x 3y 2 4xy Ii 25x 4y 3 5x 2 Y 7 B I 1 Answer Transtutors

Answer x^24y^2=4xy x^24y^24xy=0 Using the formula (ab)^2=a^2b^22ab here a=x,b=2y so, (x2y)^2=0 x2y=0 x=2y x/y=2/1समीकरण `lamda x ^(2) 4xy y ^(2) lamda x 3y 2=0` परवलय निरूपित करता है यदि `lamda ` का मान है If 2x^2lambdax y^2y^2(lambda4)x6y5=0,Dy/dx P(x)y=Q(x) So we form an Integrating Factor;

The Line X 2 4xy Y 2 0 And X Y 4 Are The Sides Of An Equilateral Triangles Whose Area Is Equal To A 3 1 2 Then A Is Equal To Sarthaks Econnect Largest Online Education Community

Binomial Theorem Wikipedia

Canonical form of a elliptical paraboloid;

Solved 7 Find All Stationary Points Of The Function F X Y Chegg Com

Solve The Bernoulli Equation Xy Y 4xy 2 With Initial Condition Y 1 4 Study Com

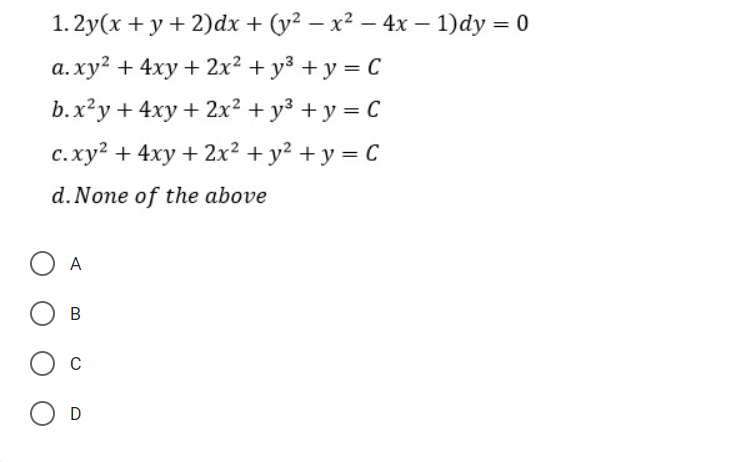
Answered 2y X Y 2 Dx Y X 4x 1 Dy Bartleby

Exact Equations Example 3 Video Khan Academy

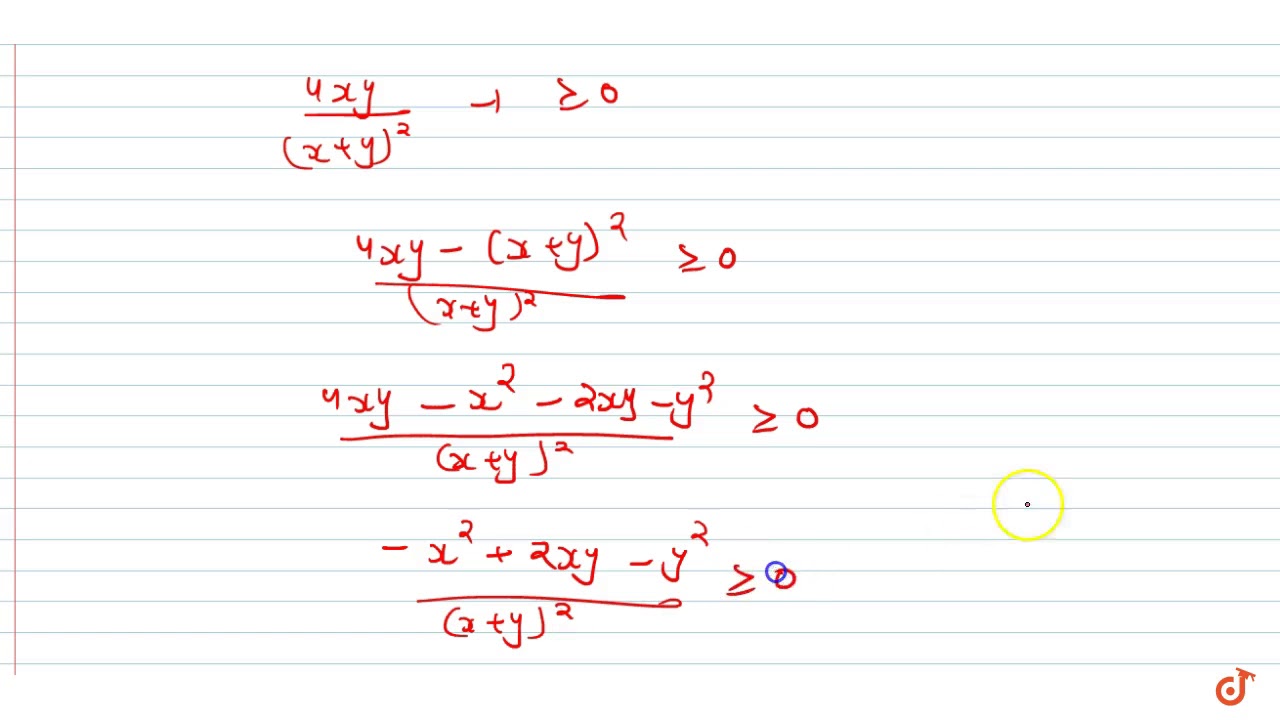
Show That The Equation Sec 2 Theta 4xy X Y 2 Is Only Possible When X Y Youtube

X 1 2 3 And Y 1 2 3 Then The Value Of X 2 4xy Y 2 X Y Integral Point

A Opq Is Formed By The Pair Of Straight Lines X 2 4xy Y 2 0 And The Line Pq The Equation Of Pq Is X Y 2 0 Sarthaks Econnect Largest Online Education Community

In Order To Eliminate The First Degree Terms From The Equation 2x 2 4xy 5y 2 4x 22y 7 0 The Point To Which Origin Is To Be Shifted Is

Quadratic Simultaneous Equations 3 Exercises Variation Theory

Solution Sqrt Studypool

Inequality Of Arithmetic And Geometric Means Wikipedia

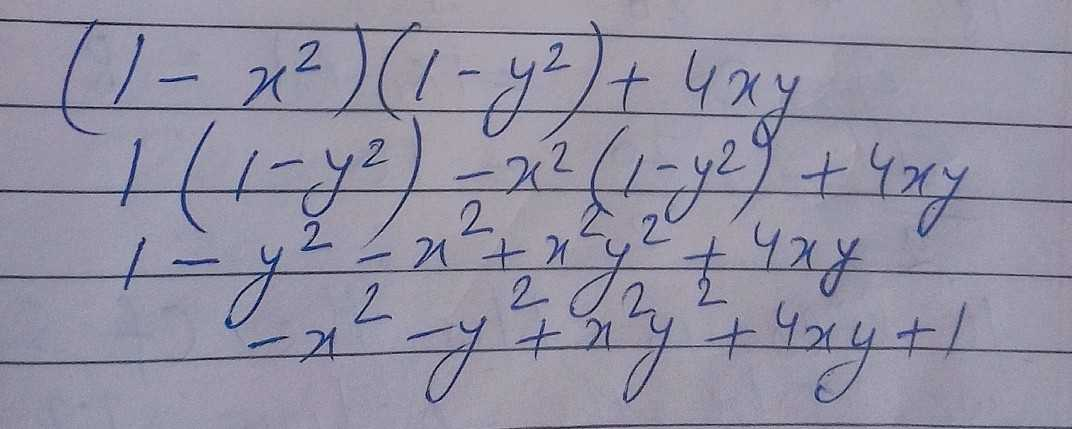
Factorise 1 X 2 1 Y 2 4xy Scholr

Find The Value Of K If X Y 2 K 4xy 3y 2 4xy 3y 2 Brainly In

2 Math With Jm Home

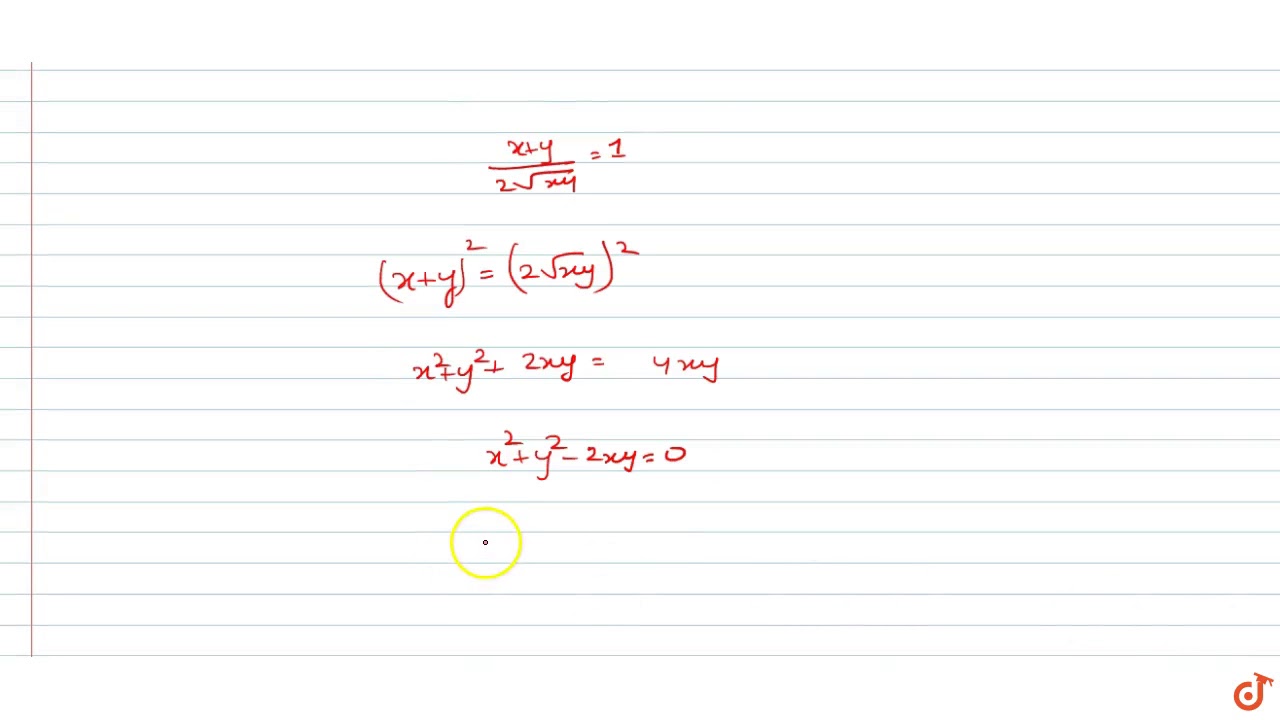
If Sec 2 Theta 4xy X Y 2 Then How Many Pairs Of X And Y Are There For Which The Condition Youtube

Rd Sharma Solutions For Class 7 Maths Chapter 7 Algebraic Expressions Download Free Pdf

Solved For The Equation 4x Y Xy 1 X Y 0 We Look For Chegg Com

Work Sneetno S Q 1 Evaluate The Following By Usin Gauthmath

Factorize X Y 2 4xy

Cauchy Riemann Show That U V X Y X2 4xy Y2 Find F Z Youtube

5 Arrange The Following Expressionsnhorizontally And Add I 10x 2 3x 11 4x 2 8x 16 Ii 24x 2 6xy 7y 2 4 3y 2 8xy 5 2x 2 Iii 8xy 7yz 10 4xy 6xz 4 Iv 3a 2 4ab 7b 2 6b 2 5a 2 Snapsolve

Complete The Proof Drag And Drop The Expression To Correctly Complete The Proof Of The Polynomial Brainly Com

Worked Example Implicit Differentiation Video Khan Academy

Solve These Simultaneous Equations 2x 3y 13 4x Y 2 Brainly Com

Q5 Solve The Following Questions S I Solve Quadratic Equation Sqrt 2 X 2 7x 5sqrt 2 0 By Using Quadratic Formula D Oth Torm Of On A P Are nd X Resnectivelv Eind Which Term Snapsolve

If Sec 2 A 4xy X Y 2 Prove That X Y And X Is Not Equal To 0 Brainly In

Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy

Sin 2 Theta X Y 2 4xy Where X Y In R Gives Theta If And Only If Youtube

Answered Consider The Following 2x2 4xy 2y Bartleby

Factorising X Y 2 4 X Y Z 2 We Gee A Quad X Y

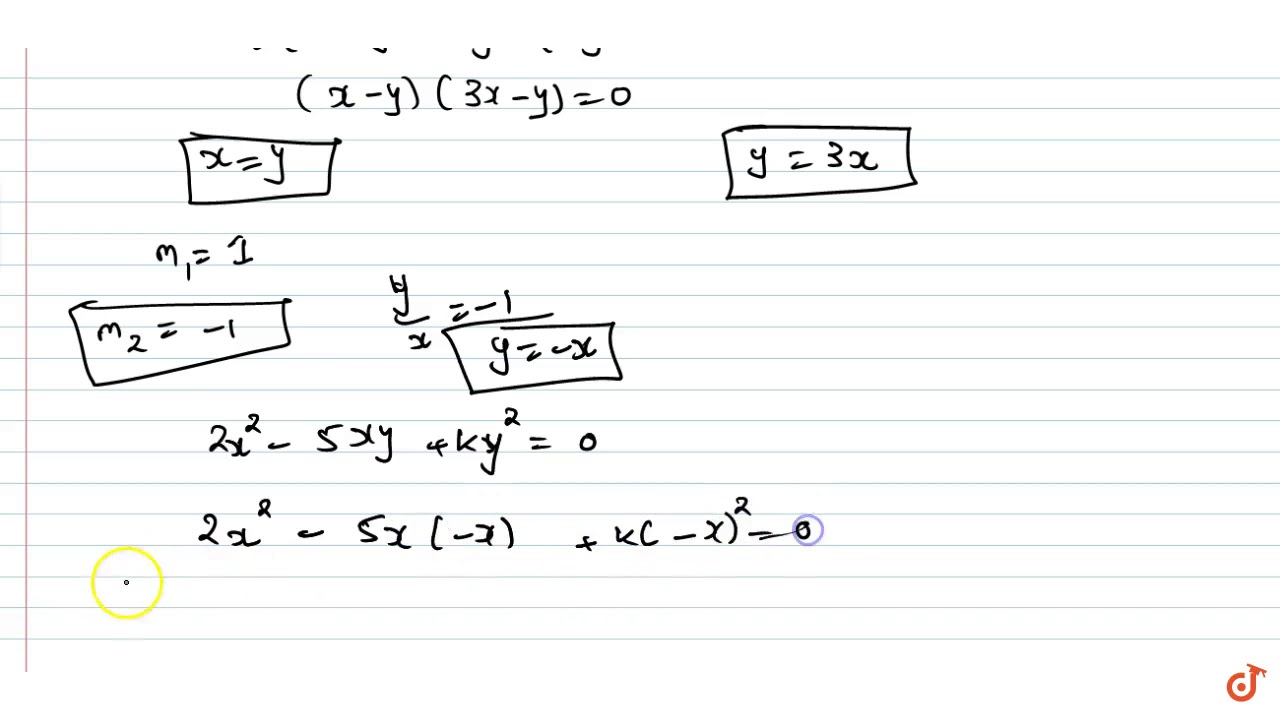
If One Of The Lines Represents By 3x 2 4xy Y 2 0 Is Perpendicular To One Of The Line 2x 2 5 Youtube

X 1 2 3 And Y 1 2 3 Then The Value Of X 2 4xy Y 2 X Y Mathematics

Useful Algebra Formulas For Competitive Exams Pdf

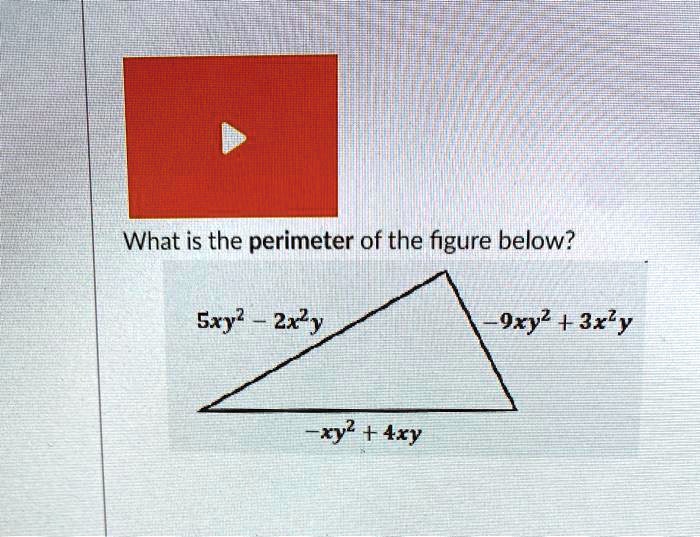
Solved What Is The Perimeter Of The Figure Below Sxy2 Zx2y 9xy2 4 3xky Xy2 4xy

Solved Evaluate The Surface Integra F X Y Z Ds Using An Explicit Representation Of The Surface F X Y 2 4xy S Is The Plane 2 1 X Y In The First Octant Set Up The Surface

Toppr Ask Question

How Do You Graph The Conic X 2 4xy Y 2 1 0 By First Rotations The Axis And Eliminating The Xy Term Socratic

Algebra Homework Please Help R Askmath

2

Solved The Haycock Formula For Approximating The Surface Chegg Com

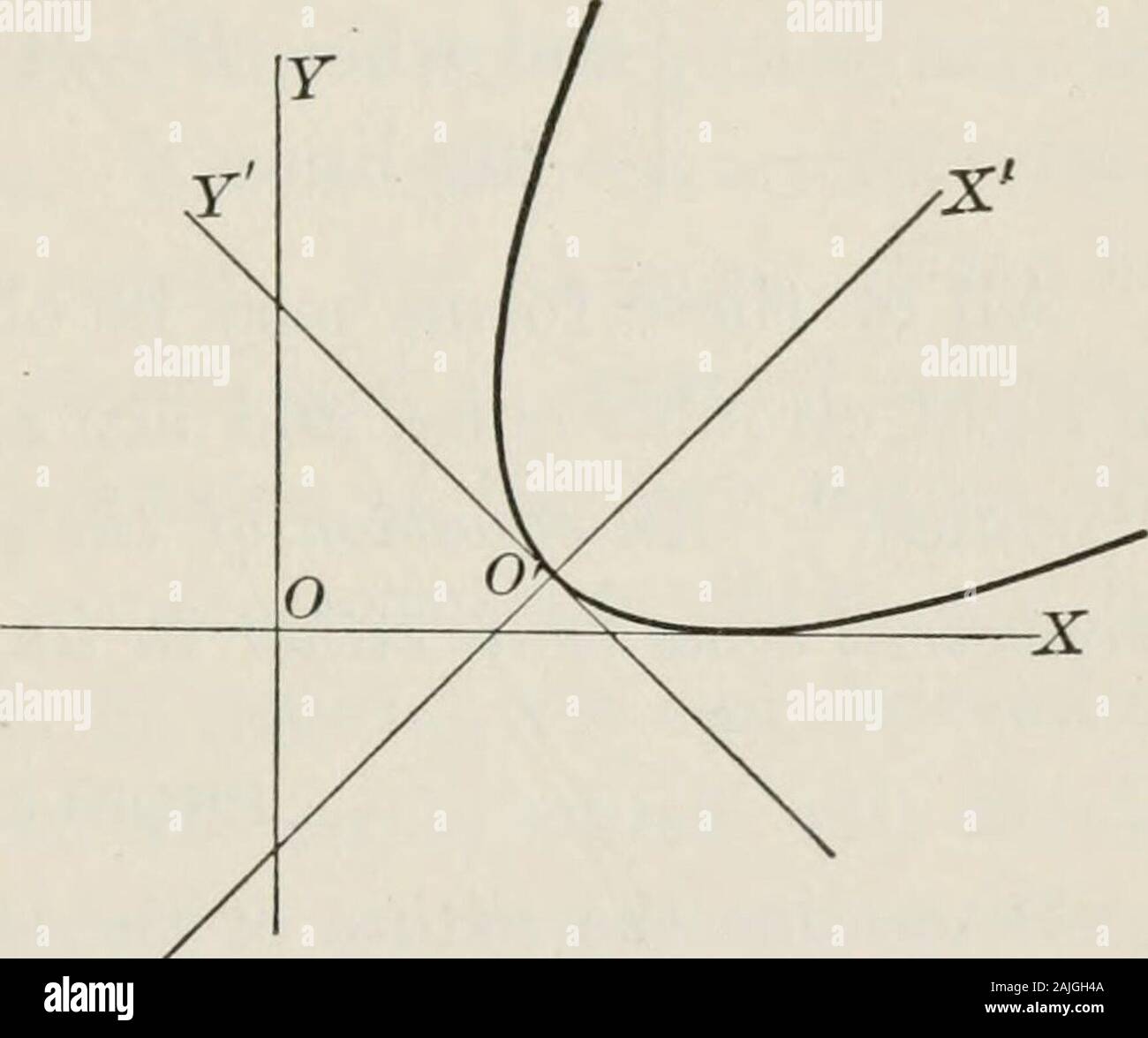
Plane And Solid Analytic Geometry An Elementary Textbook Dicular To Each Other K 2 Substituting Thisvalue In The Equation And Transposing It Becomes X Y 2y 4 X Y 3 Dividing

Gradient And Intercept Geometry Copy And Complete The Tables On The Next Slides Reminder The Equation Of A Straight Line Is Given By Y Mx C Where Ppt Download

2

Conic Section From Expanded Equation Ellipse Video Khan Academy

Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf

Solved Write The Appropriate Rotation Formulas S0 That In Rotated Ayatom The Equation Has No Xy Term 15 2 24xy 8y2 30x 40y 45 Eliminate The Parameter Find Rectangular Equation For The Planc Curve

Answered Factor X2 4xy 5y2 We Will Assume Bartleby

Factorise The Following Expression X Y 2 4xy Brainly In

Example 21 Factorize 4x2 Y2 Z2 4xy 2yz 4xz Examples

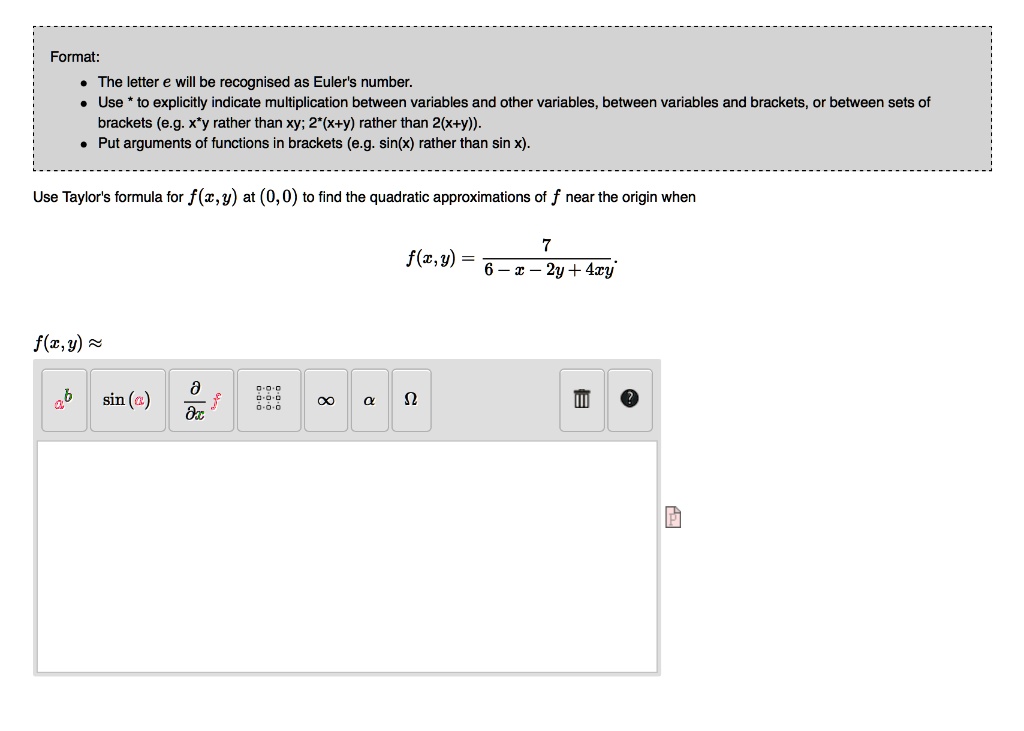
Solved Format The Letter Will Be Recognised As Euler S Number Use To Explicitly Indicate Multiplication Between Variables And Other Variables Between Variables And Brackets Or Between Sets Of Brackets E G X Y Rather Than

Tinkutara Equation Editor Math Forum Question

What Is The Value Of Y When X Is 6 The Equation Is Y 2 1x 12 Quora

Show That The Lines X 2 4xy Y 2 0 And X Y 4 Form An Equilateral Triangle Also Find The Area Of The Triangle

Solved Answer The Differential Equation From 1 11 By A Chegg Com

Solved For The Non Homogeneous Differential Equation X 2y 4xy 6y 2x 4 X 2 A Show That X 2 X 3 Each Satisfy The Homogeneous Differential Equa Course Hero

Misc 7 Show That General Solution Is X Y 1 A 1 X Y 2xy

Today S Class Derivatives Of Multivariate Functions Ppt Download

Binomial Theorem Maths Help

Q 22 If X Y 2 5 Then Frac 3x 2y 4x Y Snapsolve

Find All Points Of Intersection Of The Graphs Of X 2 4x Y 5 And X Y 9 Study Com

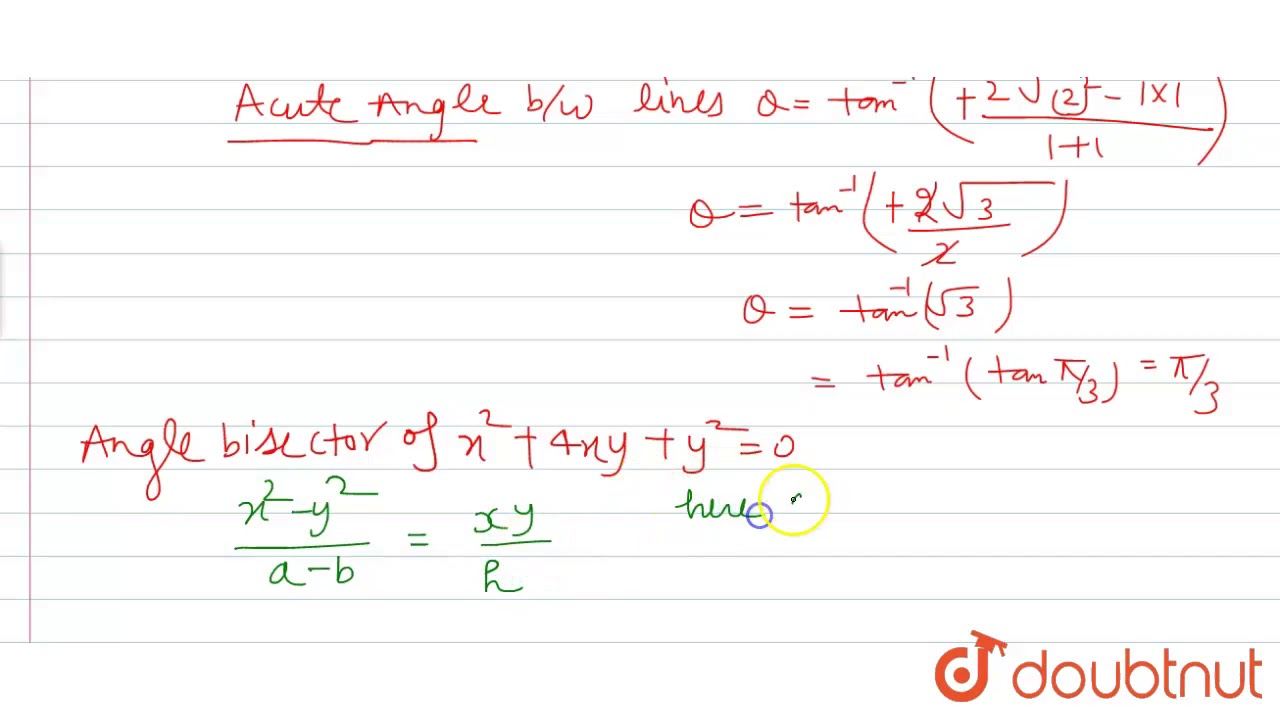
The Equation X Y 4 And X 2 4xy Y 2 0 Represent The Sides Of Youtube

X 1 2 3 And Y 1 2 3 Then The Value Of X 2 4xy Y 2 X Y Integral Point

Solved 1 Find And Sketch The Domain Of The Following Chegg Com

Is The Equation Of Math X Y 2 X Y 2 0 Math Correct Quora

View Question Rotate The Axes

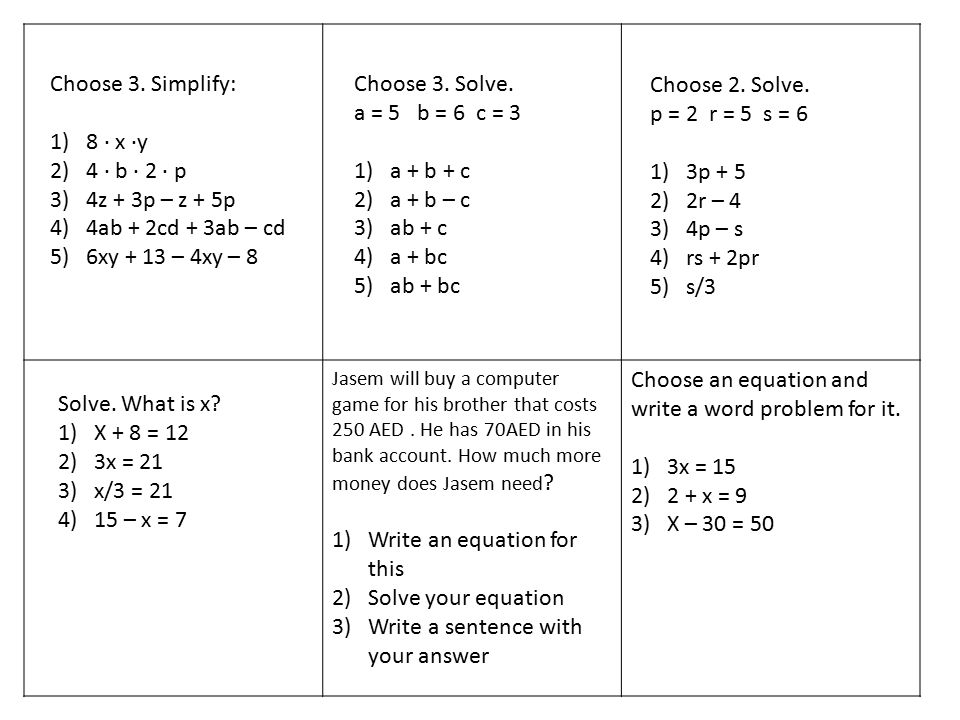
Jasem Will Buy A Computer Game For His Brother That Costs 250 Aed He Has 70aed In His Bank Account How Much More Money Does Jasem Need 1 Write An Equation Ppt Download

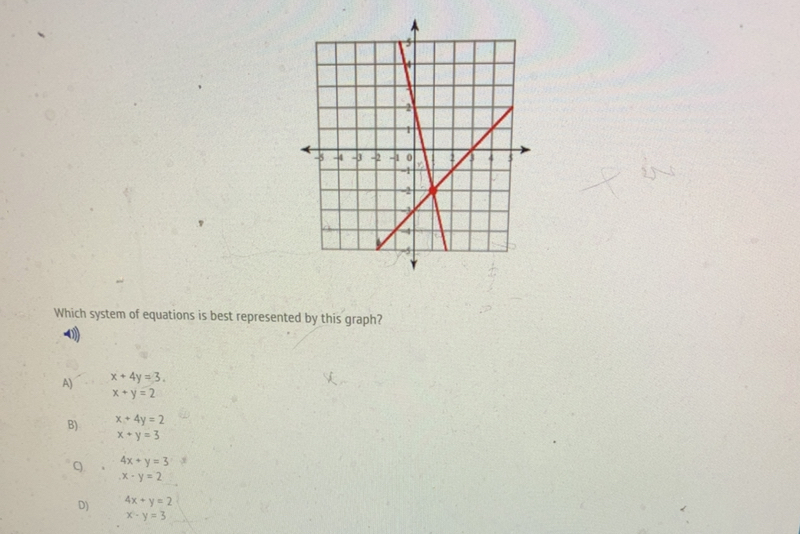
Answered Which System Of Equations Is Best Bartleby

Incoming Term: (x+y)^2-4xy formula,